Завдання до гри "Уникуб"

Завдання до гри Уникуб

Завантажити та роздрукувати
60 завдань до інтелектуальної гри "Уникуб" з книги Нікітіна.
Малюнки і тексти

Як зробити "Уникуб" своїми руками >>>

Гра "Уникуб" (Система Нікітіних)

Придбати >>

Краща з ігор для розвитку математичних здібностей допоможе у засвоєнні арифметики, алгебри і геометрії.
Гра допомагає оволодіти графічною грамотністю, розуміти ще до школи план, карту, креслення.

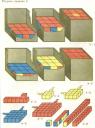
Завдання до гри "Уникуб"

У-1. Склади кубики в коробку. З самими маленькими (1,5 - 3 роки) краще починати з укладання кубиків в коробку. "Давай складемо так, щоб всі денце у коробці було червоним!" - і, звичайно, зрадіти, що вийшло добре. Засмучує малюків тільки кубик без червоних граней. Його можна укласти останнім в середині, щоб було схоже на ліхтарик.

У-2. Хто зуміє скласти кубики так, щоб денце було синім, серединка - жовтої, а верх - червоним? Малюкові можна показати малюнок у книзі.

У-3. Червоний поїзд. Потрібно скласти з кубиків поїзд, як показано на рисунку. Дахи, стіни вагонів і електровоз - червоні (з тих сторін, які видно на малюнку). Покладіть, а краще поставте або повісьте вертикально перед малюком малюнок У-1. Довжина поїзда може бути і така, як на рисунку, і більше. Це залежить від настрою "машиніста". Головна трудність завдання для малюка - одночасно стежити за двома площинами і до того ж відбирати підходящі кубики (з 2 і 3 червоними гранями). Якщо раніше він виконував завдання "Склади візерунок", завдання для нього буде відносно легким. Але якщо він зробить червоними тільки дахи вагонів, а стінки вийдуть не у всіх вагонів червоними - похваліть його.

- Добре малярі пофарбували даху - всі червоні. А тепер подивимося, як малярі пофарбували стінки.
І "ідіть" вказівним і середнім пальцями вздовж поїзда. Зупиніться біля вагону зі стінкою іншого кольору і подумайте: "Посилати вагон у перефарбовування чи ні?" Рішення повинен прийняти сам "машиніст".

У-4. Жовта квадратна коробка. Малюк повинен вирішити, які кубики треба взяти, щоб і 4 бічні грані були жовтими? Варіанти - синя і червона коробки.

В-5. Хто складе квадратну майданчик з 9 кубиків. Це майданчик для дошкільнят. Всі 4 бічні її межі жовті.

В-6. Синя квадратна майданчик з 16 кубиків. Це може бути спортмайданчик для школярів. Усі грані, крім нижньої, - сині.

В-7. Червона квадратна майданчик з 25 кубиків - це сцена для літнього театру. Тут вже треба розрізняти, які "сорти" кубиків треба укладати по периметру і які у центр моделі, інакше може не вистачити кубиків потрібного кольору.

У-8. Класифікація за червоним. Розкладіть кубики по "сортів" або краще зробити "три потяги". У першому поїзді всі вагони з одного червоним дахом, у другому - з червоними дахами і однією червоною стінкою, в третьому - з червоним дахом і двома червоними стінками. Виходять три "складу" різної довжини і один "тепловоз" (кубик без червоних граней).

З класифікації починається серйозне оволодіння "Уникубом", тому її можна дати значно раніше, тобто після виконання перших трьох завдань, особливо в тому випадку, якщо малюк вже рахує до 3 - 5 і може розрізняти "сорти" кубиків. Ми не придумали назви кожного сорту" кубиків і користуємося плодами дитячого словотворчості: "однушка червона", "двушка синя", "трійка жовта" і "нулівка". У такому назві ясно видно, за яким кольором йшла класифікація і скільки граней цього кольору є на кубику. Малюків така термінологія влаштовує, і, складаючи квадратну сцену літнього театру (У-6), вони відразу кажуть: "По кутках я поставлю "червоні троячки", між ними "червоні двійки", а в середину можна класти "червоні однушки" і що залишиться".
Попередня класифікація кубиків червоного, синього чи жовтого кольору значно полегшує виконання будь-якого завдання, тому часто малюки з власної ініціативи, перед тим як приступити до нового завдання, роблять таку класифікацію. При цьому вони вже розуміють, який колір краще вибрати і робити класифікацію повністю або відібрати одні "трійки" або "двійки".

В-9. Порахуйте, скільки вагонів у поїзді, де у вагонів тільки червоні дахи (скільки в "Уникубе" червоних "однушек"). Скільки вагонів у поїзді з червоними дахами і однією червоною стінкою? (Скільки червоних "двійок"?) Скільки вагонів у третьому поїзді? (Скільки червоних "трійок"?) З кубиків якогось "сорти" можна скласти малий куб (з 8 кубиків одного кольору?

У-10. Три бігові доріжки на стадіоні з 9 кубиків різного кольору. Бічні грані мають колір прилеглої доріжки.

У-11. Хто складе синю букву П? Малюки можуть стежити тільки за кольором букви, а старшим можна додати: склади так, щоб стінки були такими ж, як на малюнку В-11.

В-12. Червона літера Н. Так само можна складати будь-які літери, які добре виходять з кубиків (Р, Е, О, С, Т, Ч і ін).

У-13. Триколірна лавка для електрички. На жаль, на невидимій стороні тільки сидіння лавки можна зробити того ж кольору, що і на видимій, а спинки виходять іншого.

У-14. Лицарський замок з 4 баштами по кутах.

У-15. Атомний криголам з червоною палубою, синіми бортами і жовтими палубними надбудовами.

В-16. Різнобарвна фортеця з бійницею.

В-17. Циркова драбинка з синіми ступенями з двох сторін. Скільки кубиків треба для такої драбинки?

У-18. Шахова дошка 5Х5 з жовто-червоними клітинами. Чотири бічні грані теж з шахової забарвленням. Можливі варіанти: червоно-синій, жовто-синя.

У-19. Єгипетська піраміда. Праві і ліві стінки - червоні, передні і задні - жовті, "даху" всіх ярусів - сині. Для піраміди не обов'язково мати 30 кубиків, цілком достатньо 27 кубиків. Задайте малюкові завдання: як побудувати міцну піраміду, якщо 3 кубиків не вистачає? Де можна заощадити ці кубики? (Замість 4 центральних кубиків в 1 ярусі можна поставити 1 в центрі ("гробниця фараона") та повернути його на 45 градусів, щоб на нього спиралися відразу 5 кубиків 11 ярусу.)

У-20. Жовте шосе розміром 3Х9 з одним червоним квадратом в центрі. Чотири бічні грані - жовті.

У-21. Червоний п'ятиповерховий будинок з віконцями, з синіми дахами на всіх поверхах і червоними полами у всіх кімнатах. Задня стіна будинку та стіни кімнат можуть бути будь-якого кольору.

У-22, 23, 24. Три водонапірні башти різної висоти. Крім дотримання порядку фарбування тут є ще "секрет" технології будівництва. Без відкриття цього "секрету" побудувати 2-ю, а особливо 3-ю вежу дуже важко. Нехай малюк сам відкриє цей "секрет". ("Секрет" полягає в порядку складання: спочатку треба заготовити всі поверхи, але складання слід починати з верхнього поверху, а не з нижнього, як прийнято у всякому будівництві.)

У-25. Хто швидше складе малий куб червоного кольору? Всі 6 граней повинні бути червоними. Варіанти: жовтий і синій куби. На жаль, їх не можна скласти одночасно, а тільки послідовно.

У-26. Малий куб трьох кольорів. По 2 сусідні (прилеглі) межі однакового кольору (куб Вадика Склері, 6 років).

У-27. Малий куб двох кольорів. Три грані, що утворюють одну вершину, - сині, три інші - жовті. Варіанти: жовто-червоний і червоно-синій.

У-28. Малий куб трьох кольорів. Протилежні грані одного кольору (куб Вадика Склері, 6 років).

В-29. Малий куб двох кольорів. Нижня, задня і верхня межі синього кольору, а ліва, передня і права - червоного. Варіанти - інші поєднання кольорів.

У-30. Синя вокзальна лавка. З усіх боків вона пофарбована в синій колір (крім "дна"). Можна скласти таку ж лавку червоного або жовтого кольору.

У-31. Червоний колодязь. Зовні він з усіх боків червоний, а всередині - синій ("вода"). На жаль, для внутрішнього фарбування бракує однієї синьої межі і в колодязі видно "пісок" (одна жовта грань).

У-32. Крісло з підлокітниками. Обтягнуте зовні синім, а всередині і спереду червоним оксамитом. Кольори оббивки можна змінювати.

У-33. Антошина лавка. Скільки осіб можуть сісти на лавку одночасно (кожен кубик - сидіння). Сидіння і спинки з одного боку - червоні, з іншого - сині, а верх і торці - жовті (лавка Антона Нікітіна, 7 років).

У-34. Рахунок. Чому кубиків з 1 червоною межею тільки 6? (За кількістю граней куба.) Чому кубиків з 2 червоними гранями - 12? (По числу ребер куба). Чому кубиків з 3 червоними гранями - 8? (По числу вершин куба.) Чому кубиків без червоних граней тільки 1? Скільки граней у одного кубика? Хто швидше підрахує, скільки червоних граней на всіх кубиках? Скільки всіх граней на всіх кубиках? Скільки граней у 6 кубиків, у 8 кубиків, 12 кубиків, у 27?

У-35. Великий куб червоного кольору. Перевірте, чи всі 6 граней червоного кольору, так як часто (особливо ті, хто складає вперше) забувають, що "дно" повинно бути такого ж кольору, як і інші грані. Можна складати великий синій і великий жовтий куби.

Це одне з найбільш часто повторюваних завдань і завдань, які роблять "на час". Складання у 3 - 4-річних йде 10 хвилин, у 5 - 6-річних - до 2 хвилин, а 10 - 12-річні діти можуть виконати це завдання навіть за 1 хвилину. "Рекордсмени", працюючи двома руками відразу і за певною системою, можуть "вийти з хвилини".

У - 36. Великий куб трьох кольорів. Дві сусідні грані однакового кольору.

У-37. Великий триколірний куб з протилежними гранями одного кольору.

У-38. Великий триколірний куб з горизонтальними шарами одного кольору.

У-39. Двоколірний куб, 3 грані, що утворюють вершину, - жовтого кольору, 3 інші - синього. Можливі інші поєднання кольорів: жовтого з червоним, червоного з синім.

У-40. Великий двоколірний куб. Нижня, задня і верхня межі синього кольору, а ліва передня і права - червоного (куб Саші Дунаєва, 6 років). Можна використовувати і інші поєднання кольорів.

У-41. Висотний будинок жовтого кольору на 20 квартир. У підставі - 4 кубики, і висота - 5 поверхів. Стіни, дах та підлогу на 1-му поверсі жовтого кольору. Фарбування будинку можна робити і червоною і синьою.

У-42. Великий куб з шахової забарвленням всіх 6 граней. Поєднання кольорів можуть бути й інші: синьо-червоні, жовто-червоні.

У-43. Хто швидше складе червоний хрест на всіх 6 гранях? Вершини куба можуть бути й жовтими, й синіми.

У-44. Хто швидше складе букву П на всіх 6 гранях? Колір букв на протилежних гранях однаковий. Можуть бути варіанти: всі букви одного кольору (червоні, жовті, сині).

У-45. Хто швидше складе букву Н на всіх 6 гранях? Колір букв на протилежних гранях однаковий. Придумайте інші варіанти.

У-46. Склади триповерховий червоний будинок на 9 квартир, але так, щоб задня стінка була синьою. Це може бути підготовка до роз'ємним завдань, де працює "внутрішній порядок".

У-47. Великий роз'ємний червоний куб. Всі 6 зовнішніх граней - червоні, будь-які дотичні межі роз'єму - одноколірні (жовті або сині). Можливі варіанти іншого кольору.

Це завдання вирішальне у багатьох відношеннях. По-перше, виконавши його, можна переконатися, що забарвлення "Уникуба" при виготовленні була безпомилковою. По-друге, дитина, що впорався із завданням У-47, зможе впоратися і з будь-яким іншим.
Цікаво, що тренування у вирішенні завдання У-47 лише в самій початковій стадії помітно покращує результати дорослих, а потім вони змінюються мало, і дорослі взагалі, як правило, не можуть дійти до результатів, наведених дітьми вже в 10 - 12 років (відстають за часом у 2 - 3 рази). Виключення тут вкрай рідкісні.

У-48. Подвійна класифікація. Кубики спочатку треба розкласти по "сортів", як в завданні В-8, по червоному кольору. Вийде ряд з однією червоною межею (До-1), ряд з двома червоними краями (К-2) та ряд з трьома червоними краями (К-3).

Потім усередині кожного ряду розкласти їх по сортам, але вже синього (або якщо треба - жовтого) кольору. Ближче до себе покласти кубики з трьома синіми гранями, далі - з двома і ще далі - з однією. Виходять "тріади", як на У-43. Подвійна класифікація помітно полегшує виконання найскладніших завдань N 44 - 50, так як відразу можна знайти кубик з заданим числом і кольором граней. Наприклад, всі "троячки червоні" лежать в ряді К-3, "троячки сині" - це найближчі до дитини кубики (їх просто не видно), а "троячки жовті" - найдальші в кожному ряду.

У-49. Малий роз'ємний куб червоного кольору. Будь-які межі роз'єму одного кольору (куб Антона Нікітіна, 8 років). Варіанти: жовтий куб, синій куб.

У-50. Двостороння шахова дошка, розміром 5Х5 (У-46). Всі 6 граней мають шахову забарвлення. Велика, невидима на малюнку грань повинна бути червоно-жовтого або жовто-синій, а вузькі грані - тієї ж забарвлення, що і одна з широких. На рис. 46 усі вони червоно-сині. Це одне з найскладніших завдань. При його виконанні майже все роблять помилки і втрачають масу часу на їх виправлення, перестановку кубиків (дошка Сергія Бєляєва, 14 років).

У-51. Великий червоний куб. Будь-які дотичні межі роз'єми різного кольору. Зовні цей куб такий же, як У-47, але "внутрішній устрій" у нього інше - дотичні межі роз'єму - різного кольору. Зовнішнє забарвлення можна задавати і іншого кольору (жовту або синю), але тоді відповідно змінюється і внутрішнє забарвлення (куб Антона Нікітіна, 10 років).

В-52. Великий червоний куб. Будь-які дотичні межі роз'єму - смугасті. Можливі 6 варіантів: три варіанти визначаються кольором зовнішнього фарбування (червоний, жовтий, синій), і всередині кожного з них є по два варіанти внутрішньої забарвлення за роз'ємів. Один, показаний на малюнку-завдання, при якому стикаються в кожному роз'ємі різнокольорові смуги (сині з жовтим), і другий - коли стикаються смуги одноколірні (куб Антона Нікітіна, 10 років).

У-53. Хто складе великий куб так, щоб:

- у фронтальних площинах всі зовнішні та внутрішні грані були одноколірні (2 жовтих, 2 червоних, 2 синіх);
- в бічних площинах (праворуч, ліворуч і в паралельних перетинах між ними) смугасті, триколірні (6 граней);
- в горизонтальних площинах (зверху, знизу і в перетинах між ними шахової забарвлення, двоколірні (6 граней)? (Куб Володі і Наташі Лисун з Києва).

У-54. Великий червоний куб. Всі 12 дотичних граней роз'єми мають шахову забарвлення. Тут так само можна змінювати колір зовнішніх граней, а дотичні межі роз'єму або можуть бути дзеркальним відображенням один одного, або стикатися різнокольоровими квадратиками, як У-50 (куб Антона Нікітіна, 10 років).

У-55. Хто складе великий куб, щоб всі зовнішні межі попарно протилежні були одноцветны;- всі внутрішні грані роз'єму, дотичні, попарно одноколірні? (Куб Толі Заверняева, 19 років).

У-56. Хто складе великий куб так, щоб всі зовнішні та всі грані роз'ємів (12) утворили букву О. т. е. 6 червоний, 6 жовтих і 6 синіх літер? (Куб Олі Нікітіної, 17 років).

У-57. Хто складе великий куб так, щоб по всіх 18 зовнішнім і внутрішнім граням були літери Н (6 синіх, 6 червоних, 6 жовтих)?

У-58. Хто складе великий куб так, щоб на його зовнішніх гранях були червоні хрести, а на внутрішніх гранях роз'єму 6 синіх і 6 жовтих? (Куб Вані Нікітіна, 10 років)

У-59. Хто складе великий куб так, щоб всі зовнішні і всі внутрішні грані роз'єму (18 граней) були смугасті триколірні? (Куб Толі Заверняева, 19 років).

У-60. Хто складе великий куб найвищої складності? Всі 6 зовнішніх граней і 12 внутрішніх мають шахову забарвлення. Якщо зовні 6 червоно-синіх, то 6 внутрішніх червоно-жовті і ще 6 синьо-жовті (Куб Антона Нікітіна, 19 років).

З книги Нікітіна "Розвиваючі ігри"